
Desde la óptica
Como sabemos, el praxinoscopio esta compuesto por tambores concéntricos, en donde el exterior contiene una serie de imágenes consecutivas y el interior -más alto que el exterior- esta compuesto de espejos planos, formando un polígono regular como se puede apreciar en la imagen a un costado.
El número de imágenes debe ser igual al número de espejos, y estos deben quedar frente a frente para conseguir el efecto óptico al rotar el tambor.

Figura n°!: Praxinoscopio. Recuperada desdehttps://hemisferium.info/167-large_default/praxinoscopio-mini-classic-black.jpg
Hoy sabemos que la naturaleza de la luz es descrita con un modelo dual:
- La luz al propagarse lo hace en forma de onda
- La luz al interactuar con la materia lo hace como una partícula (fotón.)
Teniendo en cuanta eso, es que la luz posee dos importantes leyes que influyen en el praxinoscopio:
1° ley de reflexión de la luz
El ángulo de incidencia es igual al ángulo de rflexión, el cual se mide perpendicularmente a la superficie reflectora
2° ley de reflexión de la luz
El rayo incidente como el reflejado están en el msimo plano


Figura n°2: Reflexión en espejos planos. Recuperado desde https://www.correodelmaestro.com/publico/html5062018/capitulo2/recursos/265_02_02.jpg
Entonces al emplear espejos planos, es que se genera una imagen virtual generado por las proyecciones de los rayos de luz, de igual tamaño, derecha en la vertical y a la misma distancia entre el objeto y el espejo.
Un claro ejemplo es el siguiente diagrama de un michi frente a espejo.
Figura n°3: Gato reflejado en un espejo plano. Recuperado desde https://www.correodelmaestro.com/publico/html5062018/capitulo2/recursos/265_02_03.jpg
Efectos sobre la visión
Persistencia retiniana:
El Oxford English and Spanish Dictionary, Thesaurus, and Spanish to English Translator indica lo siguiente "Fenómeno óptico por el cual la retina conserva durante cierto tiempo la impresión de las imágenes, y por esta razón se perciben con natural continuidad las películas cinematográficas, sin advertir las transiciones de una imagen a otra." (párr. 1)

Figura n°3: Demostración de fotogramas seguidos
Recuperada desde https://docsjo.files.wordpress.com/2015/07/giphy-3.gif
A lo anterior, es que podemos decir que esta percepción del movimiento aparente o real es un proceso cerebral de nuestro sistema de visión según Oviedo (La definición del concepto de percepción en psicología, 2004). Es así, que este fenómeno se genera a partir de los 16 fotogramas o cuadros por segundo (o abreviadamente, fps).
Como referencia, el cine mudo vio sus inicios con 24 fps y hoy en día los videojuegos de PS3 y XBOX 360 generalmente llegan a 60 fps cuando no hay interacción o cuando hay escenarios poco contrastados en objetos u acción; pero una vez que hay acción, bajan y son casi estables en 30 fps.

Fundamentos
físicos
La física detrás de un juguete óptico

Fenómeno phi

Szigety, Tintori, Viau y Moro (2010) declaran lo siguiente:
Cuando dos imágenes casi idénticas se proyectan sucesivamente con un intervalo de tiempo muy corto se tiene la sensación de estar frente a un objeto que se desplaza de una posición a otra. Éste es un ejemplo del fenómeno phi, que consiste en que el cerebro crea una sensación de movimiento aunque reciba solamente pequeños fragmentos del mismo. Es decir, rellena los huecos entre ellos y crea la ilusión de un continuo, a partir de la simple serie de imágenes estáticas del movimiento. (pág 567, párr. 2)
Mientras la persistencia retiniana produce una superposición de imágenes, el fenómeno phi reconstruye los tramos entre las imágenes sumando las correspondientes unidades (impresiones) una detrás de otra. De esta manera se genera la sensación de movimiento.
(pág. 567, párr. 3)
Figura n° 4: Demostración del fenómeno phi. Recuperada desde http://4.bp.blogspot.com/-ku7XzPJTOwQ/Tx6a_9c3ddI/AAAAAAAAB2w/K9LM88aIzqo/s1600/loading.gif
Frecuencia crítica de fluctuación
Szigety, Tintori, Viau y Moro (2010) afirman que se llama así a la frecuencia mínima de parpadeo que tiene que tener una fuente de luz fluctuante para producir sensación de luz continua en nuestros ojos.(pág. 567, párr. 4).
La persistencia retiniana y el fenómeno phi conjuntamente imponen una condición a cualquier fuente luminosa que produzca imágenes o impulsos. Su frecuencia de fluctuación tiene que tener un valor mínimo (crítico) para que se pueda apreciar la luz emitida como continua. Esta frecuencia es de 50 veces por segundo; una frecuencia inferior produce parpadeo (pág. 567, párr. 5).
Video n°1: Comparación fps en el cine.
Recuperado desde https://www.youtube.com/watch?v=3x9_QvtNrrk
Lo anterior explica que cuando estes jugando Lol a 30 fps, presentes discontinuidad en la imágen; mientras que si juegas a 60 fps, la imagen es completamente fluida a pesar de caídas de 2 a 3 fps. Y si no juegas LOL, es que te recomendamos ver el video n°1 sobre comparación de fps en el cine
Movimiento Circular Uniforme (MCU)
Según el libro de cpech (2018), un movimiento circular uniforme, es un movimiento de trayectoria circular en el que la velocidad angular es constante. Esto implica que describe ángulos iguales en tiempos iguales. En él, el vector velocidad no cambia de módulo pero sí de dirección (es tangente en cada punto a la trayectoria). Esto quiere decir que no tiene aceleración tangencial y aceleración angular, aunque sí aceleración normal. (pág. 36, capítulo 2)
Con el apoyo del texto cpech, se plantea que en el movimiento circular uniforme existen características que se determinan durante el recorrido que realiza este, tales como:
-
Periodo (T): Es el tiempo que tarda el cuerpo en dar una vuelta completa, midiéndose en unidades de tiempo.

Siendo dos pi la vuelta completa y w la velocidad angular.
2. Frecuencia (f): Es el número de revoluciones por unidad de tiempo, donde se expresa de la siguiente forma.
.png)
La frecuencia es inversa al periodo y su unidad es el hercio.
3. Velocidad angular (w): Se denomina velocidad angular al cociente entre el desplazamiento y el tiempo, cuya unidad es rad/s.

Figura n°5: Gráficamente la velocidad angular es un vector perpendicular al plano de movimiento.
En el instante final del recorrido del objeto, este se encontrara en la posición final dada por el angulo final . El objeto se habrá desplazado en cierto intervalo de desplazamiento de angulo en el intervalo de tiempo.
.png)
4. Magnitud de la rapidez: La rapidez (v) permanece constante, siendo el módulo de la velocidad tangencial.
.png)
Relación de un objeto rotando de forma circular con radio y con periodo T.
5. Velocidad tangencial: Es la representación vectorial de la dirección tangente presente en la circunferencia. Al cambiar su dirección su vector también cambia. Entonces esta variación por unidad de tiempo de la velocidad, implica que debe existir una aceleración en ese punto en cuestión.

.png)
la unidad de medida de la velocidad tangencial es de m/s.
6. Aceleración centripeta: En este movimiento de trayectoria circular, sólo está sometido a una única aceleración, que apunta siempre hacia el centro de rotación, y esta es la aceleración centrípeta y se denota por ac y su unidad en el S.I se representa por metro sobre segundo al cuadrado

Para obtener la relación de su formula, se realizan los siguientes cálculos:

por triángulos equivalentes tenemos:
.png)
.png)
por tanto, tenemos:
.png)
.png)

Finalmente, se tiene que la aceleración centripeta, esta dirigida al centro de la circunferencia:
.png)
7. Fuerza centripeta: Si consideramos la masa de un objeto giratorio porque se ve afectado por la aceleración ac, entonces según la segunda ley de Newton, tenemos:
.png)
El cuerpo está sometido a una fuerza que tiene la misma dirección y sentido que la aceleración centrípeta. Esta fuerza apunta al centro de rotación y se denomina fuerza centrípeta, asignándose por Fc. Lo que provoca esta fuerza, es que hace cambiar la dirección de la velocidad tangencial, evitando que el cuerpo en sí, siga con un movimiento rectilíneo uniforme.
.png)
Teniendo en cuenta que el valor de la aceleración centrípeta es la velocidad al cuadrado partida por el radio de la trayectoria, reemplazamos los valores, obteniendo el valor escalar de la fuerza centrípeta, en relación con la velocidad angular y el radio.
.png)
Movimiento Armónico Simple (MAS)

Figura n°7: Movimiento circular visto como un movimiento socilatorio de ida y vuelta. Recuperado desde http://rincondelaciencia.educa.madrid.org/Curiosid/Rc-28/mcuani.gif
Debido a las características que queremos lograr en el praxinoscopio para su correcto funcionamiento, es que presenta en su movimiento circular uniforme una velocidad y masa constante.
Con la ayuda de Tippensa (2011), es que podemos decir que visto de otra forma, sería una partícula que gira en un círculo de radio constante con rapidez uniforme, como lo vemos en la figura n°7 a un costado. No obstante, una persona que observa el movimiento desde el borde de la mesa lo ve como un movimiento oscilatorio de ida y vuelta, y ello corresponde precisamente a un MAS (pág. 286).
Este MAS sería una proyección horizontal en donde el radio del círculo es igual a la amplitud de la oscilación tal como vemos en la figura n°8 a un costado.
Es así cómo podemos determinar relaciones que nos permitan predecir la posición, la velocidad y el desplazamiento en función del tiempo, pero debido a que estas pueden compararse con un MAS.
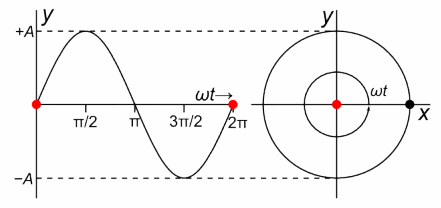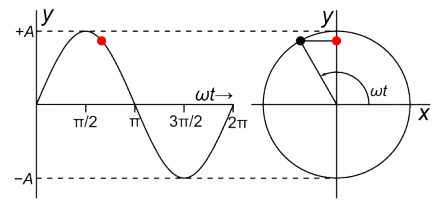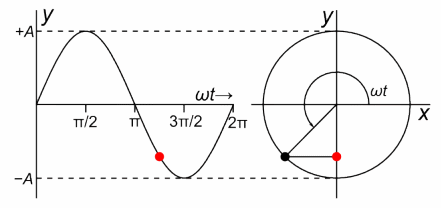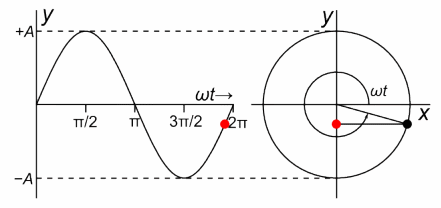
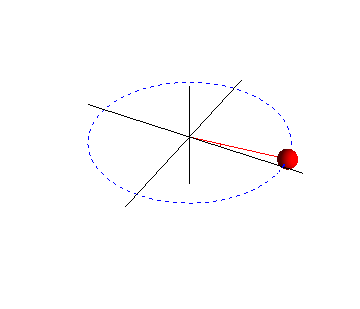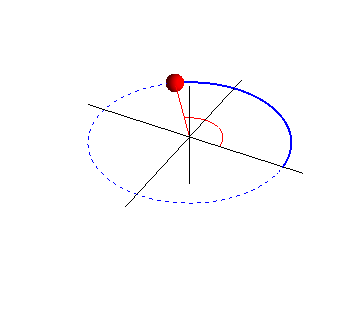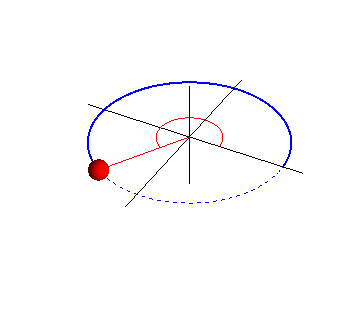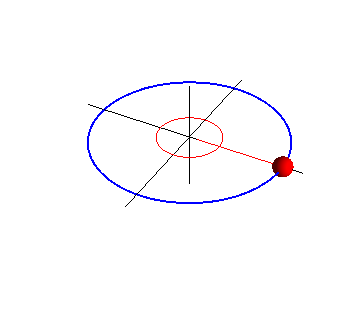
Figura n°8: Proyección horizontal de un MCU . Recuperado desde https://lh4.googleusercontent.com/proxy/Auz3gC94lE0MGXZXUvW9tOtiK01gsqiUmb-vfEOTMJhl4ICYfOCZdpHXAgwOb_FpIlhHvlZoUzs5IQIFFYdHE_3wBKltoWtqKTJ2bUkblAYOEkg0O6B6T_pmAMIx-zwqXyqCb7IFZBCvj5JxcQ=w1400

Puesto que es el movimiento de la proyección el que deseamos estudiar, nos referiremos aquí a la posición P del objeto que se mueve en círculo como el punto de referencia. Si la rapidez lineal vT y la velocidad angular del punto de referencia son constantes, entonces la proyección Q se moverá de un lado al otro con MAS, donde en un tiempo t, el punto de referencia P se habrá movido a lo largo de un ángulo . El desplazamiento x de la proyección Q es, por tanto,
Figura n°9: Circulo de referencia de un desplazamiento en el movimiento de un MAS. Recuperado desde https://gc.scalahed.com/recursos/files/r145r/w484w/U9_archivos/Nueva_U9_Liga2_clip_image002.jpg
Como el ángulo theta es igual a t, ahora podemos escribir el desplazamiento como una función de la velocidad angular del punto de referencia:
También hemos de recordar que la velocidad angular se relaciona con la frecuencia de revolución mediante:
Como sabemos que a frecuencia es constante, podemos reemplazar:
Esta ecuación puede aplicarse para calcular el desplazamiento de un cuerpo que se mueve con un MAS de amplitud A y frecuencia f.
Siguiendo con la ayuda de Tippens (2011) es que nos dice que para obtener la velocidad, es que debemos tener en cuenta que la dirección del cuerpo que oscila se invierte en los puntos extremos de su movimiento, su velocidad debe ser cero cuando su desplazamiento es máximo.
Así, en general es que la velocidad de este cuerpo en cualquier punto Q se determina a partir del círculo de referencia de esta forma:
El signo es negativo en virtud de que la dirección de la velocidad es hacia la izquierda. Podemos dar una forma más conveniente a la ecuación si recordamos la relación entre la velocidad tangencial y la velocidad angular:
Sustituyendo, es que nos queda:
Con esta ecuación se obtiene la velocidad de un cuerpo que oscila en cualquier instante si se tiene presente que el seno de theta es negativo cuando el punto de referencia queda por debajo del diámetro del círculo de referencia.
Así, si pudieramos ver en una sola gráfica la posición y velocidad del praxinoscopio visto desde un MAS, es que veríamos una gráfica parecida a esta:
Engranajes
Figura n° 10: Gráfica de posición y velocidad en un MAS.
Recuperado desde http://laplace.us.es/wiki/images/6/62/Fasorxv.gif
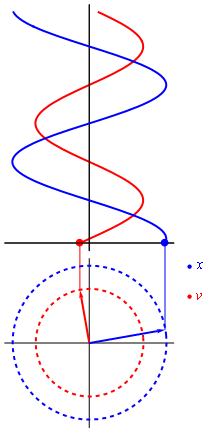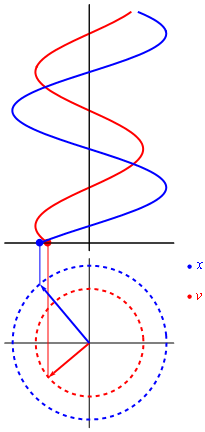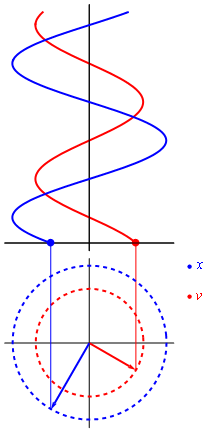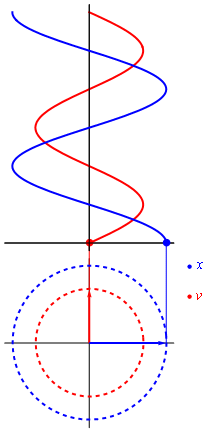
Debido a cuestiones visibles, es que se grafica en azul la posición y en rojo la velocidad.
Además, debido a que la posición es calculada con el coseno y la velocidad con el seno, es que presentan un desface de pi medios

Según el documento de la universidad de Cantabria sobre la cinemática y dinámica de maquinas, y la tesis realizada por Gustavo Fernando Chasi (2012), el objetivo primordial de los engranajes es transmitir una rotación entre dos ejes con una relación de velocidades angulares constantes.
Así se suele hablar de par de engranajes, ruedas dentadas o engrane, donde se refiere a la unión que se utiliza con este mecanismo, donde es utilizado para transmitir potencia mecánica entre estos dos ejes del engranaje, mediante un contacto directo entre ellos.
En los engranajes, se encuentran conceptos físicos importantes, los cuales se basan en la “ley fundamental de los engranajes”. La ley general de engranajes describe cuál debe ser la forma de los dientes de engranes entrelazados (acoplados) para asegurar la mejor transmisión posible de movimiento rotatorio uniforme. En este movimiento uniforme, existe una “relación de transmisión” entre ellos, donde el cociente entre la velocidad angular de salida w2 (velocidad de rueda conducida) y la de entrada w1 (velocidad de rueda conductora), además de que existirá una razón entre los radios de entrada de entrada y de salida.

Relación de transmisión

En este contexto se utilizaran los engranajes para lograr reducir la velocidad angular que genera la potencia mecánica a elevadas revoluciones del motor y así poder aprovecharla de mejor manera, manteniendo la velocidad constante. Para lograr esta relación de transmisión y reducción en el mecanismo, se toma en cuenta la velocidad de rotación de la rueda motriz o conductora y el número de dientes del engranaje.
_edited.png)
Donde n es la velocidad de la rueda motriz y Z el numero de dientes del engranaje